False Discovery Rate

Overview

This page briefly describes the False Discovery Rate (FDR) and provides an annotated resource list.

Description

When analyzing results from genomewide studies, often thousands of hypothesis tests are conducted simultaneously. Use of the traditional Bonferroni method to correct for multiple comparisons is too conservative, since guarding against the occurrence of false positives will lead to many missed findings. In order to be able to identify as many significant comparisons as possible while still maintaining a low false positive rate, the False Discovery Rate (FDR) and its analog the q-value are utilized.

Defining the problem
When conducting hypothesis tests, for example to see whether two means are significantly different, we calculate a p-value, which is the probability of obtaining a test statistic that is as or more extreme than the observed one, assuming the null hypothesis is true. If we had a p-value of 0.03, for example, that would mean that if our null hypothesis is true, there would be a 3% chance of obtaining our observed test statistic or a more extreme. Since this is a small probability, we reject the null hypothesis and say that the means are significantly different. We usually like to keep this probability under 5%. When we set our alpha to 0.05, we are saying that we want the probability that a null finding will be called significant to be less than 5%. In other words, we want the probability of a type I error, or a false positive, to be less than 5%.

When we are conducting multiple comparisons (I will call each test a “feature”), we have an increased probability of false positives. The more features you have, the higher the chances of a null feature being called significant. The false positive rate (FPR), or per comparison error rate (PCER), is the expected number of false positives out of all hypothesis tests conducted. So if we control the FPR at an alpha of 0.05, we guarantee than the percentage of false positives (null features called significant) out of all hypothesis tests is 5% or less. This method poses a problem when we are conducting a large number of hypothesis tests. For example, if we were doing a genomewide study looking at differential gene expression between tumor tissue and healthy tissue, and we tested 1000 genes and controlled the FPR, on average 50 truly null genes will be called significant. This method is too liberal, since we do not want to have such a great number of false positives.

Typically, multiple comparison procedures control for the family-wise error rate (FWER) instead, which is the probability of having one or more false positives out of all the hypothesis tests conducted. The commonly used Bonferroni correction controls the FWER. If we test each hypothesis at a significance level of (alpha/# of hypothesis tests), we guarantee that the probability of having one or more false positives is less than alpha. So if alpha was 0.05 and we were testing our 1000 genes, we would test each p-value at a significance level of 0.00005 to guarantee that the probability of having one or more false positives is 5% or less. However, guarding against any single false positive may be too strict for genomewide studies, and can lead to many missed findings, especially if we expect there to be many true positives.

Controlling for the false discovery rate (FDR) is a way to identify as many significant features as possible while incurring a relatively low proportion of false positives.

Steps for controlling for false discovery rate:

• Control for FDR at level α *(i.e. The expected level of false discoveries divided by total number of discoveries is controlled)

E[V⁄R]

• Calculate p-values for each hypothesis test and order (smallest to largest, P(min)…….P(max))

• For the ith ordered p-value check if the following is satisfied:

P(i) ≤ α × i/m

If true, then significant

*Limitation: if error rate (α) very large may lead to increased number of false positives among significant results

The False Discovery Rate (FDR)

The FDR is the rate that features called significant are truly null.
FDR = expected (# false predictions/ # total predictions)

The FDR is the rate that features called significant are truly null. An FDR of 5% means that, among all features called significant, 5% of these are truly null. Just as we set alpha as a threshold for the p-value to control the FPR, we can also set a threshold for the q-value, which is the FDR analog of the p-value. A p-value threshold (alpha) of 0.05 yields a FPR of 5% among all truly null features. A q-value threshold of 0.05 yields a FDR of 5% among all features called significant. The q-value is the expected proportion of false positives among all features as or more extreme than the observed one.

In our study of 1000 genes, let’s say gene Y had a p-value of 0.00005 and a q-value of 0.03. The probability that a test statistic of a non-differentially expressed gene would be as or more extreme as the test statistic for gene Y is 0.00005. However, gene Y’s test statistic may be very extreme, and maybe this test statistic is unlikely for a differentially expressed gene. It is quite possible that there truly are differentially expressed genes with test statistics less extreme than gene Y. Using the q-value of 0.03 allows us to say that 3% of the genes as or more extreme (i.e. the genes that have lower p-values) as gene Y are false positives. Using q-values allows us to decide how many false positives we are willing to accept among all the features that we call significant. This is particularly useful when we wish to make a large number of discoveries for further confirmation later on (i.e. pilot study or exploratory analyses, for example if we did a gene expression microarray to pick differentially expressed genes for confirmation with real-time PCR). This is also useful in genomewide studies where we expect a sizeable portion of features to be truly alternative, and we do not want to restrict our discovery capacity.

The FDR has some useful properties. If all null hypotheses are true (there are no truly alternative results) the FDR=FWER. When there is some number of truly alternative hypotheses, controlling for the FWER automatically also controls the FDR.

The power of the FDR method (recall that power is the probability of rejecting the null hypothesis when the alternative is true) is uniformly larger than Bonferroni methods. The power advantage of the FDR over the Bonferroni methods increases with an increasing number of hypothesis tests.

Estimation of the FDR
(From Storey and Tibshirani, 2003)

Definitions:t: thresholdV: # of false positivesS: # of features called significantm0: # of truly null featuresm: total # of hypothesis tests (features)
The FDR at a certain threshold, t, is FDR(t). FDR(t) ≈ E[V(t)]/E[S(t)] –> the FDR at a certain threshold can be estimated as the expected # of false positives at that threshold divided by the expected # of features called significant at that threshold.
How do we estimate E[S(t)]?
E[S(t)] is simply S(t), the number of observed p-values ≤ t (i.e. the number of features we call significant at the chosen threshold).The probability a null p-value is ≤ t is t (when alpha=0.05, there is a 5% probability that a truly null feature has a p-value that is below the threshold by chance and is therefore called significant).
How do we estimate E[V(t)]?
E[V(t)]=m0*t –> the expected number of false positives for a given threshold equals the number of truly null features times the probability a null feature will be called significant.
How do we estimate m0?
The true value of m0 is unknown. We can estimate the proportion of features that are truly null, m0/m = π0.
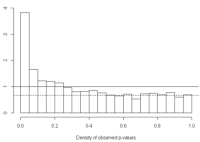
We assume that p-values of null features will be uniformly distributed (have a flat distribution) between [0,1]. The height of the flat distribution gives a conservative estimate of the overall proportion of null p-values, π0. For example, the image below taken from Storey and Tibshirani (2003) is a density histogram of 3000 p-values for 3000 genes from a gene expression study. The dotted line represents the height of the flat portion of the histogram. We expect truly null features to form this flat distribution from [0,1], and truly alternative features to be closer to 0.

π0 is quantified as 

where lambda is the tuning parameter (for example in the image above we might select lambda=0.5, since after a p-value of 0.5 the distribution is fairly flat. The proportion of truly null features equals the number of p-values greater than lambda divided by m(1-lambda). As lambda approaches 0 (when most of the distribution is flat), the denominator will be approximately m, as will the numerator since the majority of the p-values will be greater than lambda, and π0 will be approximately 1 (all features are null).
The choice of lambda is usually automated by statistical programs.

Now that we have estimated π0, we can estimate FDR(t) as

The numerator for this equation is just the expected number of false positives, since π0*m is the estimated number of truly null hypotheses and t is the probability of a truly null feature being called significant (being below the threshold t). The denominator, as we said above, is simply the number of features called significant.
The q-value for a feature then is the minimum FDR that can be attained when calling that feature significant.

(Note: the above definitions assume that m is very large, and so S>0. When S=0 the FDR is undefined, so in the statistics literature the quantity E[V/S|S>0]*Pr(S>0) is used as the FDR. Alternatively, the positive FDR (pFDR) is used, which is E[V/S|S>0]. See Benjamini and Hochberg (1995) and Storey and Tibshirani (2003) for more information.)

Readings

Textbooks & Chapters

“RECENT ADVANCES IN BIOSTATISTICS (Volume 4):
False Discovery Rates, Survival Analysis, and Related Topics”
Edited by Manish Bhattacharjee (New Jersey Institute of Technology, USA), Sunil K Dhar (New Jersey Institute of Technology, USA), & Sundarraman Subramanian (New Jersey Institute of Technology, USA).
http://www.worldscibooks.com/lifesci/8010.html
This book’s first chapter provides a review of FDR controlling procedures that have been proposed by prominent statisticians in the field, and proposes a new adaptive method that controls the FDR when the p-values are independent or positively dependent.

“Intuitive Biostatistics: A Nonmathematical Guide to Statistical Thinking”
by Harvey Motulsky
http://www.amazon.com/Intuitive-Biostatistics-Nonmathematical-Statistical-Thinking/dp/product-description/0199730067
This is a book of statistics written for scientists who lack a complex statistical background. Part E, “Challenges in Statistics,” explains in layman’s terms the problem of multiple comparisons and the different ways of dealing with it, including basic descriptions of the family-wise error rate and the FDR.

“Large-scale inference: empirical Bayes methods for estimation, testing and prediction” 
by Efron, B. (2010). Institute of Mathematical Statistics Monographs, Cambridge University Press.
http://www.amazon.com/gp/product/0521192498/ref=as_li_ss_tl?ie=UTF8&tag=chrprobboo-20&linkCode=as2&camp=1789&creative=390957&creativeASIN=0521192498
This is a book reviews the concept of FDR and explores its value not only as an estimation procedure but also a significance-testing object. The author also provides an empirical evaluation of the accuracy of FDR estimates.

Methodological Articles

Benjamini, Y. and Y. Hochberg (1995). “Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing.” Journal of the Royal Statistical Society. Series B (Methodological) 57(1): 289-300.
This 1995 paper was the first formal description of FDR. The authors explain mathematically how the FDR relates to the family-wise error rate (FWER), provide a simple example of how to use the FDR, and conduct a simulation study demonstrating the power of the FDR procedure compared to Bonferroni-type procedures.

Storey, J. D. and R. Tibshirani (2003). “Statistical significance for genomewide studies.”Proceedings of the National Academy of Sciences 100(16): 9440-9445.
This paper explains what the FDR is and why it is important for genomewide studies, and explains how the FDR can be estimated. It gives examples of situations in which the FDR would be useful, and provides a work-through example of how the authors used the FDR to analyze microarray differential gene expression data.

Storey JD. (2010) False discovery rates. In International Encyclopedia of Statistical Science, Lovric M (editor).
A very good article over-viewing FDR control, the positive FDR (pFDR), and dependence. Recommended to get a simplified overview of the FDR and related methods for multiple comparisons.

Reiner A, Yekutieli D, Benjamini Y: Identifying differentially expressed genes using false discovery rate controlling procedures. Bioinformatics 2003, 19(3):368-375.
This article uses simulated microarray data to compare three re-sampling based FDR controlling procedures to the Benjamini-Hochberg procedure. Re-sampling of test statistics is done so as not to assume the distribution of the test statistic of each gene’s differential expression.

Verhoeven KJF, Simonsen KL, McIntyre LM: Implementing false discovery rate control: increasing your power. Oikos 2005, 108(3):643-647.
This paper explains the Benjamini-Hochberg procedure, provides a simulation example, and discusses recent developments in the FDR field that can provide more power than the original FDR method.

Stan Pounds and Cheng Cheng (2004) “Improving false discovery rate estimation” Bioinformatics Vol. 20 no. 11 2004, pages 1737–1745.
This paper introduces a method called the spacings LOESS histogram (SPLOSH). This method is proposed for estimating the conditional FDR (cFDR), the expected proportion of false positives conditioned on having k ‘significant’ findings.

Daniel Yekutieli , Yoav Benjamini (1998) “Resampling-based false discovery rate controlling multiple test procedures for correlated test statistics” Journal of Statistical Planning and Inference 82 (1999) 171-196.
This paper introduces a new FDR controlling procedure to deal with test statistics that are correlated with each other. The method involves calculating a p-value based on resampling. Properties of this method are evaluated using a simulation study.

Yoav Benjamini and Daniel Yekutieli (2001) “The control of the false discovery rate in multiple testing under dependency” The Annals of Statistics 2001, Vol. 29, No. 4, 1165–1188.
The FDR method that was originally proposed was for use in multiple hypothesis testing of independent test statistics. This paper shows that the original FDR method also controls the FDR when the test statistics have positive regression dependency on each of the test statistics corresponding to the true null hypothesis. An example of dependent test statistics would be the testing of multiple endpoints between treatment and control groups in a clinical trial.

John D. Storey (2003) “The positive false discovery rate: A Bayesian interpretation and q-value” The Annals of Statistics 2003, Vol. 31, No. 6, 2013–2035.
This paper defines the positive false discovery rate (pFDR), which is the expected number of false positives out of all tests called significant given that there is at least one positive finding. The paper also provides a Bayesian interpretation of the pFDR.

Yudi Pawitan, Stefan Michiels, Serge Koscielny, Arief Gusnanto, and Alexander Ploner (2005) “False discovery rate, sensitivity and sample size for microarray studies” Bioinformatics Vol. 21 no. 13 2005, pages 3017–3024.
This paper describes a method for computing sample size for a two-sample comparative study based on FDR control and sensitivity.

Grant GR, Liu J, Stoeckert CJ Jr. (2005) A practical false discovery rate approach to identifying patterns of differential expression in microarray data. Bioinformatics. 2005, 21(11): 2684-90.
Authors describe the permutation estimation methods and discuss issues regarding researcher choice of statistic and data transformation methods. Power optimization relating to use of microarray data is also explored.

Jianqing Fan, Frederick L. Moore, Xu Han, Weijie Gu, Estimating False Discovery Proportion Under Arbitrary Covariance Dependence. J Am Stat Assoc. 2012; 107(499): 1019–1035.
This paper proposes and describes a method for the control of FDR based on a principal factor approximation of covariance matrix of the test statistics.

Application Articles

Han S, Lee K-M, Park SK, Lee JE, Ahn HS, Shin HY, Kang HJ, Koo HH, Seo JJ, Choi JE et al: Genome-wide association study of childhood acute lymphoblastic leukemia in Korea. Leukemia research 2010, 34(10):1271-1274.
This was a genome-wide association (GWAS) study testing one million single nucleotide polymorphisms (SNPs) for association with childhood actute lymphoblastic leukemia (ALL). They controlled the FDR at 0.2 and found 6 SNPs in 4 different genes to be strongly associated with ALL risk.

Pedersen, K. S., Bamlet, W. R., Oberg, A. L., de Andrade, M., Matsumoto, M. E., Tang, H., Thibodeau, S. N., Petersen, G. M. and Wang, L. (2011). Leukocyte DNA Methylation Signature Differentiates Pancreatic Cancer Patients from Healthy Controls. PLoS ONE 6, e18223.
This study controlled for an FDR <0.05 when looking for differentially methylated genes between pancreatic adenoma patients and healthy controls to find epigenetic biomarkers of disease.

Daniel W. Lin, Liesel M. FitzGerald, Rong Fu, Erika M. Kwon, Siqun Lilly Zheng, Suzanne et.al.Genetic Variants in the LEPR, CRY1, RNASEL, IL4, and ARVCF Genes Are Prognostic Markers of Prostate Cancer-Specific Mortality (2011), Cancer Epidemiol Biomarkers Prev.2011;20:1928-1936. This study examined the variation in selected candidate genes related to onset of prostate cancer in order to test its prognostic value among high risk individuals. FDR was used to rank single nucleotide polymorphisms (SNPs) and identify top ranking snps of interest.

Radom-Aizik S, Zaldivar F, Leu S-Y, Adams GR, Oliver S, Cooper DM: Effects of Exercise on microRNA Expression in Young Males Peripheral Blood Mononuclear Cells. Clinical and Translational Science 2012, 5(1):32-38.
This study examined the change in microRNA expression before and after exercise using a microarray. They used the Benjamini-Hochberg procedure to control the FDR at 0.05, and found 34 out of 236 microRNAs to be differentially expressed. The investigators then selected microRNAs from these 34 to be confirmed with real time PCR.

Websites

R statistical package
http://genomine.org/qvalue/results.html
Annotated R code used to analyze data in the Storey and Tibshirani (2003) paper, including link to data file. This code can be adapted to work with any array data.

http://www.bioconductor.org/packages/release/bioc/html/qvalue.html
qvalue package for R.

http://journal.r-project.org/archive/2009-1/RJournal_2009-1.pdf

Journal R Project is a peer-reviewed, open-access publication of the R Foundation for Statistical Computing. This volume provides an article entitled ‘Sample Size Estimation While Controlling False Discovery Rates for Microarray Experiments’ by Megan Orr and Peng Liu. Specific functions and detailed examples are provided.

http://strimmerlab.org/notes/fdr.html
This website provides a list of R software for FDR analysis, with links to their home pages for a description of package features.

SAS
http://support.sas.com/documentation/cdl/en/statug/63347/HTML/default/viewer.htm#statug_multtest_sect001.htm
Description of PROC MULTTEST in SAS, which provides options for controlling the FDR using different methods.

STATA 
http://www.stata-journal.com/article.html?article=st0209
Provides STATA commands for the computation of q values for multiple-test procedures (compute FDR adjusted q-values).

FDR_general web resources
http://www.math.tau.ac.il/~ybenja/fdr/index.htm
Website managed by the statisticians at Tel Aviv University who first formally introduced the FDR.

http://www.math.tau.ac.il/~ybenja/
This FDR website has many references available. Lecture on FDR is available for review.

http://www.cbil.upenn.edu/PaGE/fdr.html
Nice, concise explanation of FDR. A useful at-a-glance summary with example is provided.

http://www.rowett.ac.uk/~gwh/False-positives-and-the-qvalue.pdf
A brief overview of false positives and q-values.

Courses

A Tutorial on False Discovery Control by Christopher R. Genovese Department of Statistics Carnegie Mellon University.
This powerpoint is a very thorough tutorial for someone interested in learning the mathematical underpinnings of the FDR and variations on the FDR.

Multiple Testing by Joshua Akey, Department of Genome Sciences, University of Washington.
This powerpoint provides a very intuitive understanding of multiple comparisons and the FDR. This lecture is good for those looking for a simple understanding of the FDR without a lot of math.

Estimating the Local False Discovery Rate in the Detection of Diferential expression between Two Classes.
Presentation by Geoffrey MacLachlan, Professor, University of Queensland, Australia.
www.youtube.com/watch?v=J4wn9_LGPcY
This video lecture was helpful in learning about the local FDR, which is the probability of a specific hypothesis being true, given its specific test statistic or p-value.

False Discovery Rate Controlling Procedures for Discrete Tests
Presentation by Ruth Heller, Professor, Department of Statistics and Operations Research. Tel Aviv University
http://www.youtube.com/watch?v=IGjElkd4eS8
This video lecture was helpful in learning about the application of FDR control on discrete data. Several step up and step down procedures for FDR control when dealing with discrete data are discussed. Alternatives that take ultimately help increase power are reviewed.