Causal Mediation

Overview

This page briefly compares mediation analysis from both the traditional and causal inference frameworks. An annotated resource list is provided, followed by a suggested article for a future Epi 6 project relating to causal mediation.

Description

What is mediation?
Mediation is the process through which an exposure causes disease. In the simple diagram below we examine the total effect of exposure on outcome.

Researchers may hypothesize that some or all of the total effect of exposure on an outcome operates through a mediator, which is an effect of the exposure and a cause of the outcome. When a mediator is hypothesized, the total effect can be broken into two parts: the direct and indirect effect. The direct effect is the effect of exposure on the outcome absent the mediator. The indirect pathway is the effect of exposure on the outcome that works through the mediator.

Why care about mediation?
There are many motivations for performing mediation analysis, but the overarching goal is one of causal explanation. Other more specific reasons include: increasing construct validity, strengthening evidence of the main effect hypothesis, understanding the mechanisms and active ingredients by which exposure causes disease, and evaluating and improving interventions (i.e. identifying surrogate outcomes). The motivation behind a mediation analysis is relate to which effect – direct or indirect – the researcher wants to isolate and this depends on one’s research interests. For example, if a researcher is mainly interested in eliminating mediated pathways not of interest in order to strengthen their evidence of an exposure-outcome relationship, the effect of interest is the direct effect. On the other hand, if underlying mechanisms by which exposure causes disease are of interest, the researcher may be more interested in estimating the indirect effect. 

How has mediation traditionally been examined in the literature?

Qualitative approach (Baron and Kenny’s causal steps)

The traditional approach to mediation – what we have learned in the majority of our epidemiology and biostatistics classes – was proposed by Baron and Kenny in 1986 (an early version appeared in Judd and Kenny, 1981). The four steps to identification of a mediator are summarized as:

1. Test the total effect of X on Y

2. Test the relationship between X and M

3. Test the relationship between M and Y, controlling for X

4. Declare whether M is a partial or full mediator

In epidemiology the last step is commonly utilized – that is, putting your proposed mediator in a model and assessing whether there is an appreciable reduction in magnitude of the parameter estimate comparing the adjusted estimate to the crude. Typically, an arbitrary metric such as the 10% rule is used to define ‘appreciable.’

Quantitative approach (Baron and Kenny’s product method, or difference method)

One can take a more quantitative approach to mediation by obtaining an estimate of the total, direct, and indirect pathways. In the simple figures above, the estimate of the total effect is the value of the parameter estimate for the exposure when the outcome is regressed on the exposure; the direct effect is the parameter estimate for the exposure when the outcome is regressed on the exposure and the mediator.

The indirect effect can be calculated either by a product or difference method. Using the product method the parameter estimate for the exposure in the XàM model is multiplied by the parameter estimate for the mediator in the MàY model, adjusted for X (a*b). The difference method simply subtracts the direct effect from the total (c-c’) to obtain the indirect effect. Of note, because estimating the indirect effect simply requires multiplying or subtracting two parameter estimates, obtaining an estimate of the statistical significance of the indirect effect is complicated and requires hand calculation or use of a macro of some kind. 

Limitations of the traditional approach 

There are two main limitations of the traditional approach to estimating direct and indirect effects.

First, effect decomposition – the fact that the direct and indirect effects sum to the total – using the product or difference method only works in the special case where linear regression is used for the mediator and outcome models and when there is no exposure-mediator interaction. If interaction is present and the traditional approach is utilized, the effect estimates obtained will not be interpretable. One point worth noting about assessing mediation with binary outcomes when the outcome is common is that because of non-collapsibility of the odds ratio, the traditional approach to mediation even if there is no X-M interaction will result in a non-interpretable estimate. Specifically, this would give you a conservative test of mediation (see VanderWeele’s textbook for more information).

Second, an often-ignored assumption of this approach is no unmeasured confounding of the M-Y path. This assumption can be violated in both observational studies as well as RCTs because while the exposure can sometimes be randomized, it is often not the case that both exposure and mediator are randomized.

Causal Mediation 

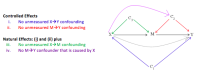
Causal inference methods for mediation analysis (“causal mediation”) are an extension of the traditional approach, developed to better address the main limitations described above. First, these methods allow for effect decomposition in the presence of X-M interaction by defining direct and indirect effects (controlled or natural) from a potential outcomes (PO) framework and developing estimations of these quantities that are not model specific. Second, causal mediation clearly explicates the four main assumptions for estimating direct and indirect effects, providing clarity to the no unmeasured confounding assumptions required to perform mediation analysis. The causal mediation approach places emphasis on conducting sensitivity analyses to examine the robustness of findings to violations of these assumptions.

There are four main assumptions in causal mediation. These assumptions are essentially the same as those required for conducting mediation analyses in the traditional framework, but they are stated clearly and up front. There are two types of direct and indirect effects: controlled and natural. To estimate controlled effects requires the first two assumptions; all four are needed to estimate natural effects.

Controlled direct and natural direct and indirect effects can be defined using PO notation and estimates can be obtained using Pearl’s mediation formulas. In the absence of interaction all direct effects are equal (and are equivalent to the traditional approach) and all indirect effects are equal. When X-M interaction is present, you obtain as many controlled direct effects as you have levels of the mediator. In contrast, in the presence of interaction, only one estimate is obtained for the natural direct effect (either pure or total) and one estimate for the natural indirect effect (either pure or total) and these estimates sum to the total effect. Whether you decide to estimate the pure or total natural direct/indirect effect depends on to which estimate you want to attribute the X-M interaction. That is, you can either estimate the pure indirect effect and the total direct effect, or the total indirect effect and the pure direct effect; depending on the chosen combination, the X-M interaction is either absorbed into the direct or indirect effect, respectively.

The PO definitions and Pearl’s equations for each effect are as follows:

PO definitions:

Controlled direct effect:

• Y1m-Y0m, where we set M=m

Natural direct effect:

• Pure: Y1M0-Y0M0

• Total: Y1M1-Y0M1

Natural indirect effect:

• Pure: Y0M1-Y0M0

• Total: Y1M1-Y1M0

Estimation of PO quantities (Pearl’s Mediation Formula)

These equations are simplified and only the pure direct and total indirect effect estimates are shown; in reality, you would need to condition on confounders in each formula as well.

Controlled direct effect:

• E[Yxm-Yx*m]=E[Y|x,m]-E[Y|x*,m]

Pure direct effect: Takes the CDE for all values of m and weights it by P(mediator|unexposed); weighting by the P(mediator|exposed) would provide an estimate of the total direct effect.

• E[YxMx*-Yx*Mx*]=∑m{E[Y|x,m]-E[Y|x*,m]}P(m|x*)

Total indirect effect

• E[YxMx-YxMx*]=∑mE[Y|x,m]{P(m|x)-P(m|x*)}

Controlled vs. natural effects

The estimation of the PO quantities highlights an area of controversy in the causal mediation literature, a debate surrounding controlled vs. natural effect estimates. Natural effects require additional assumptions to obtain estimates, and some researchers believe these assumptions are too strong. Specifically, when estimating natural effects, a ‘cross-world counterfactual’ assumption is needed, which in application is the weighting of our controlled direct effect by the proportion of the mediator among a particular level of the exposure. Controlled effects require fewer assumptions and are prescriptive in their RCT-like approach by hypothetically assigning the same value of the mediator to all individuals in the population. Some see controlled effects as having more policy relevance than natural effects (see Naimi et al, 2014).

In contrast, natural effects examine mediation from a more descriptive perspective, with emphasis on understanding the mechanisms. To do so, the mediator must be allowed to vary as it naturally would under a particular exposure condition as opposed to fixing it to a particular level for all. Though requiring more assumptions, a major benefit of the natural effects is that effect decomposition works in the presence of interaction: you can obtain both an estimate of the direct and indirect effect. This allows for an estimation of the proportion of the total effect due to the mediator (the proportion mediated) which is not possible to estimate using controlled effects, given that there as many controlled direct effects as strata of the mediator.

Application examples

The field of causal mediation is fairly new and techniques emerge frequently. Below are summaries of two easy to implement causal mediation tools in software familiar to most epidemiologists.

SAS macro

The SAS macro is a regression-based approach to estimating controlled direct and natural direct and indirect effects. This macro easily handles decomposition into direct and indirect effects in the presence of X-M interaction and allows for X, M, and Y to take on various forms: the exposure and mediator can be binary or continuous and the outcome can be continuous, binary (logistic or log-linear models), count (poisson or negative binomial models), or time-to-event (proportional hazards or accelerated failure time models). The macro can also handle data that utilize various study designs. One major benefit to using such a macro – regardless of whether or not you want to model X-M interaction – is that you obtain an estimate of the indirect effect and its level of significance in your output.

R mediation package

R’s causal mediation package, mediation, uses simulations to estimate direct and indirect effects when there is X-M interaction. It does so by modeling the interaction in the outcome regression model and using the mediate( ) function to estimate the natural direct and indirect effects based on Pearl’s mediation formula. If investigators are unsure about whether they should model X-M interaction, a formal test of X-M interaction may be conducted using the function test.TMint( ); a significant finding implies that the no X-M interaction assumption does not hold. To address the second limitation of the traditional approach, a sensitivity analysis function, medsens( ), allows for investigators to examine, through simulations, the robustness of their findings to potential unmeasured M-Y confounders. Results for all analyses are displayed using the summary( ) and plot( ) functions.

In conclusion: So, what to do… 

When there is no exposure-mediator interaction:

• Causal mediation will be equivalent to the traditional approach (so long as assumptions are met and given the other caveats about variable forms mentioned).

If exposure-mediator interaction is present:

• You can still use traditional approaches to detect the presence or absence of mediation, but if you try to estimate direct and indirect effects your estimates will be biased.

• You can estimate the natural indirect and direct effects

If you are unsure if there is exposure-mediator interaction:

• Some researchers suggest running your models both ways – with and without X-M interaction – and examining the change in estimates from model to the next (i.e. not relying solely on the significance of the X-M interaction term in the outcome regression model). If there does not appear to be an appreciable change in the magnitude of parameter estimates when X-M interaction is modeled, it might be best to stick with the simpler approach.

If you are uneasy about the no unmeasured confounding assumptions:

• If possible, limit unmeasured confounding in design phase of a study by considering mediational pathways of interest and collecting data on both X-Y AND M-Y confounders.

• Conduct sensitivity analyses to examine the robustness of the results under various scenarios of unmeasured confounding. Some programs (i.e. R) have built-in sensitivity analysis functions. Chapter 3 in VanderWeele’s textbook is devoted to ways to conduct sensitivity analyses.

Readings

Textbooks & Chapters
 

Causal Mediation

• VANDERWEELE, T. 2015. Explanation in Causal Inference: Methods for Mediation and Interaction, Oxford University Press.
  A new textbook on mediation; concise yet extensitve description of causal mediation.

Traditional Approach

• MACKINNON, D. P. 2008. Introduction to statistical mediation analysis, Routledge.
  Clear discussion of the traditional approach and its limitations.

Methodological Articles

Traditional Method:

• JUDD, C. M. & KENNY, D. A. 1981. Process Analysis: Estimating Mediation in Treatment Evaluations. Evaluation Review, 5, 602-619.

• BARON, R. M. & KENNY, D. A. 1986. The moderator-mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. J Pers Soc Psychol, 51, 1173-82.
  The original mediation articles that outline the “traditional method” and its assumptions.

• MACKINNON, D. P., FAIRCHILD, A. J. & FRITZ, M. S. 2007. Mediation analysis. Annu Rev Psychol, 58, 593-614.
  A review of statistical methods for assessing mediation beyond the approach described in Baron and Kenny.

Causal Inference Approach (Causal Mediation):

Background on causal mediation from a potential outcomes perspective:

• ROBINS, J. M. & GREENLAND, S. 1992. Identifiability and exchangeability for direct and indirect effects. Epidemiology, 3, 143-55.
  Explanation of causal mediation from a potential outcomes perspective. Outlines the different causal mediation types; helpful to read along with Hafeman 2008.

• HAFEMAN, D. M. 2008. A sufficient cause based approach to the assessment of mediation. Eur J Epidemiol, 23, 711-21.
  Explanation of causal mediation from a sufficient component cause perspective. Outlines the different mediation types; helpful in connecting between synergy and mediation. 

Motivation for causal mediation analysis:

• PEARL, J. Direct and indirect effects. Proceedings of the seventeenth conference on uncertainty in artificial intelligence, 2001. Morgan Kaufmann Publishers Inc., 411-420. (section 2)
  Provides the formulas for causal mediation. A bit dense, but a seminal paper in the understanding of causal mediation. 

• HAFEMAN, D. M. & SCHWARTZ, S. 2009. Opening the Black Box: a motivation for the assessment of mediation. Int J Epidemiol, 38, 838-45.
  Outline of the motivations of causal medation with a focus on the natural effects.

Natural vs. controlled effects:

• NAIMI, A. I., KAUFMAN, J. S. & MACLEHOSE, R. F. 2014. Mediation misgivings: ambiguous clinical and public health interpretations of natural direct and indirect effects. Int J Epidemiol, 43, 1656-61.
  A review of controlled vs. natural effects and the pros/cons of each approach.

• KAUFMAN, J. S., MACLEHOSE, R. F. & KAUFMAN, S. 2004. A further critique of the analytic strategy of adjusting for covariates to identify biologic mediation. Epidemiol Perspect Innov, 1,4.
  Explains causal mediation from a PO perspective; describes and demonstrates the issues with estimating controlled effects in the presence of interaction.

• KAUFMAN, J. S. 2009. Commentary: Gilding the black box. International Journal of Epidemiology, 38, 845-847.
  Commentary to Hafeman and Schwartz, 2009; proponent of controlled effects.

• SCHWARTZ, S., HAFEMAN, D., CAMPBELL, U. & GATTO, N. 2010. Author response. Commentary: gilding the black box. Int J Epidemiol, 39, 1399-401.
  Response to Kaufman, 2009 commentary.

Estimation of direct and indirect effects:

• PEARL, J. Direct and indirect effects. Proceedings of the seventeenth conference on uncertainty in artificial intelligence, 2001. Morgan Kaufmann Publishers Inc., 411-420. (section 3)
  Section 3 of Pearl’s 2001 article provides the formulas for estimating the controlled direct effect, natural direct effect, and natural indirect effect. Notion is dense but once you understand Pearl you can understand a lot of common mediation analytic tools that are based on his mediation formula.

• PETERSEN, M. L., SINISI, S. E. & VAN DER LAAN, M. J. 2006. Estimation of direct causal effects. Epidemiology, 17, 276-84.
  Estimation of direct effects using accessible language and formulas; good to read alongside Pearl 2001.

Application Articles
 

Estimating direct and indirect effects using a regression based framework:

SAS and SPSS

• Valeri and Vanderweele SAS Macro (available on his tools and tutorials webpage): http://www.hsph.harvard.edu/tyler-vanderweele/tools-and-tutorials/
  A how-to and background information on causal mediation using a SAS macro to estimate controlled direct, natural direct, and natural indirect effects. This article is the ‘back-bone’ paper and as additional features have been added additional papers have been published (see below).

Additional resources for survival analysis (time to event outcome)

• VANDERWEELE, T. J. 2011. Causal Mediation Analysis With Survival Data.Epidemiology, 22, 582-585.

• VALERI, L. & VANDERWEELE, T. J. 2015. SAS macro for causal mediation analysis with survival data. Epidemiology, 26, e23-4.
  The original macro from Valeri and VanderWeele was not capable of analyzing time-to-event outcome data; in March of 2015 this function became available.

Additional resources for logistic regression analysis for a binary outcome

• VANDERWEELE, T. J. & VANSTEELANDT, S. 2010. Odds ratios for mediation analysis for a dichotomous outcome. Am J Epidemiol, 172, 1339-48.
  Addition information on issues with using logistic regression to analyze binary outcome data; it is important to understand the caveats of binary outcome data when performing causal mediation analyses.

STATA

• EMSLEY, R. & LIU, H. 2013. PARAMED: Stata module to perform causal mediation analysis using parametric regression models. Statistical Software Components. http://econpapers.repec.org/software/bocbocode/s457581.htm
  The STATA version of the macro from Valeri and Vanderweele.

 MPLUS

• MUTHÉN, B. & ASPAROUHOV, T. 2014. Causal effects in mediation modeling: an introduction with applications to latent variables. Structural Equation Modeling: A Multidisciplinary Journal, 1-12.http://www.tandfonline.com/doi/pdf/10.1080/10705511.2014.935843
  Begins with an uncomplicated summary of traditional and causal mediation and then explains mediation capabilities in MPLUS.

Estimating direct and indirect effects using a simulation based framework:

R package

• IMAI, K., KEELE, L. & TINGLEY, D. 2010. A general approach to causal mediation analysis. Psychol Methods, 15, 309-34.
  Background information on the theory underlying the simulation based approach to causal mediation in R. This is helpful to have as a reference to help understand how estimates are created when working through the R vignette. It is also helpful in understanding what estimates are provided in the output.

• TINGLEY, D., YAMAMOTO, T., HIROSE, K., KEELE, L. & IMAI, K. 2014. Mediation: R package for causal mediation analysis. http://cran.r-project.org/web/packages/mediation
  The R vignette for performing causal mediation.

STATA module

• HICKS, R. & TINGLEY, D. 2011. Causal mediation analysis. Stata Journal, 11, 605-619. http://www.stata-journal.com/article.html?article=st0243
  The STATA verion of the R package.

Sensitivity analyses:
Sensitivity analyses are an important part of conducting causal mediation analyses since strong assumptions are required to obtain natural effects. These articles discuss various sensitivity analyses related to the different assumption of causal mediation. In addition, see Chapter 3 of VaderWeele’s textbook.

• HAFEMAN, D. M. 2011. Confounding of indirect effects: a sensitivity analysis exploring the range of bias due to a cause common to both the mediator and the outcome. Am J Epidemiol, 174, 710-7.

• VANDERWEELE, T. J., VANSTEELANDT, S. & ROBINS, J. M. 2014. Effect decomposition in the presence of an exposure-induced mediator-outcome confounder.Epidemiology, 25, 300-6.

Moving mediation analysis beyond regression based approaches (an idea for future Epi 6 project):

• LANGE, T., VANSTEELANDT, S. & BEKAERT, M. 2012. A simple unified approach for estimating natural direct and indirect effects. Am J Epidemiol, 176, 190-5.
  Describes the use of marginal structural models as a tool to estimate direct and indirect effects.

Websites

Four-part lecture from Tyler VanderWeele: Harvard’s Biostatistics Seminar Series

Part 1: https://vimeo.com/harvardcatalyst/review/123625538/7fd460d231

Part 2: https://vimeo.com/harvardcatalyst/review/123625537/7241c2dd4e

Part 3: https://vimeo.com/harvardcatalyst/review/123625539/d70731540c

Part 4: https://vimeo.com/harvardcatalyst/review/123625540/00f720c86f

A review of the recent causal mediation literature and practical application tools from Tyler VanderWeele. 

David Kenny’s website: http://davidakenny.net/cm/mediate.htm
An overview of mediation from both a traditional and causal mediation standpoint.